#一、竞品调研

目前，家政行业仍然以线下为主，大多数的家政公司还是采用人工指派（家政派单老师/经纪人）的方式进行派单，不过像58到家、天鹅到家这些规模较大的互联网家政平台早已引入了需求预测和自动化派单系统来实现精细化运营。经过调研，我们发现UU家政和58到家的派单场景整体上是比较相似的，以下是58到家派单问题的业务抽象（内容来自2022年MathorCup高校数学建模挑战赛——大数据竞赛 赛道A试题）：

1、约束条件及假设：

• 所有订单都要分配一个且只有一个阿姨；
• 每个订单需要指定一个服务开始时间，这个时间的取值范围为[最早时间，最晚时间]，且是半点的整数倍；
• 一个阿姨同时只能服务一个订单；
• 阿姨需要在每个订单的服务开始时间之前到达客户位置；
• 阿姨每天开始任务时必须从初始点位置出发；

2、优化目标：

• 所有订单匹配的阿姨的服务分，其平均值A 尽可能大；
• 最小化每单的平均通行距离B。一个订单的通行距离指的是阿姨从上一个地点到本单地点的距离（欧式距离），其中阿姨第一个订单的通行距离等于从初始点到第一个订单位置的距离，单位是千米；
• 最小化阿姨服务订单的平均间隔时间C。一个订单的间隔时间指的是，阿姨从上一个单服务结束时刻到本单服务开始时刻的时间间隔，单位是小时，其中阿姨第一个订单的间隔时间设定为0.5 小时（阿姨首单需要做基本的准备工作，不考虑阿姨从初始点到第一个订单的通行时间）；
• 总体目标是最大化各个目标的加权和：αA-βB-γC。

#二、模型构建

由于家政订单大多为带预约时间段的订单，因此对于家政派单问题，我们可以将其看作一种带时间窗的车辆路径问题（Vehicle Routing Problem with Time Windows, VRPTW），它是运筹学上经典的车辆路径问题（Vehicle Routing Problem, VRP）的一个变种问题，VRPTW可以简单描述为：配送中心需要向一批位置已知、需求已知的顾客点提供货物，并由一批车队负责货物的配送，目标是组织适当的行车路线，使每个顾客点的需求均被满足，并在顾客要求的时间窗口内将货物送达，并且使车队所有车辆的配送成本（cost）最低。

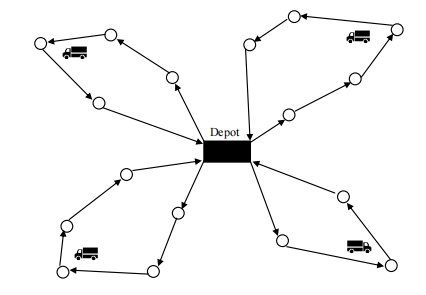
在家政派单问题中，可以将获取到的家政订单看作要配送的货物，将跑男看作参与配送的车辆，将跑男设置的初始接单位置看作配送中心，而订单的预约服务时间段就是货物要求送达的时间窗口，我们的目的就是决定订单和跑男的匹配结果，使得各项约束均被满足（因为时间约束的存在，订单和跑男的匹配结果也决定了跑男服务订单的顺序，即行驶路线），且使得整体的派单成本最小，在我们的家政问题中，定义了两类需要优化的“成本”：（1）为了提高服务质量，要最大化所有订单匹配跑男的平均服务分，服务分是基于跑男上一个周期内的接单量、客户评价等指标计算的来衡量跑男服务质量的权重分数；（2）最小化跑男每单的平均行驶距离。

由此，可以建立起家政派单问题的数学模型如下：

1、集合：

2、决策变量：

3、模型参量：

4、目标函数与约束条件（仅展示部分约束）：

• 每个进行服务的家政跑男都必须具有该订单所需的技能；
• 每个订单只能分配给一个家政跑男完成；
• 家政跑男的接单总数不能超过其本月可接单的最大数量限制；
• 跑男要在订单的最晚开始时间前到达顾客点；
• 订单的服务时间要在跑男的可接单时间范围内。

需要注意的是，我们的派单问题和VRPTW的区别在于：（1）路径规划问题中的订单往往是在同一个时间段内的，制定好配送路径后，车辆一定是以路径中的上一个节点为起点连续行驶至下一个节点；而由于家政订单是有很长的预约期限的，可能同批进行指派的订单不在同一天，这时就要考虑新分配的订单是否为当天的首单，如果是首单则默认是以跑男的初始接单位置为起点（为了简化表达，上面的数学模型中没有体现这一点）；（2）传统的路径规划问题中所有车辆在初始状态都是完全空闲的，而在我们的问题中家政跑男身上可能有之前已分配的订单占用排期，还有请假、开工状态等与跑男可接单时段有关的因素，需要考虑的情形更加复杂。

#三、算法设计

#1、常用的求解算法介绍

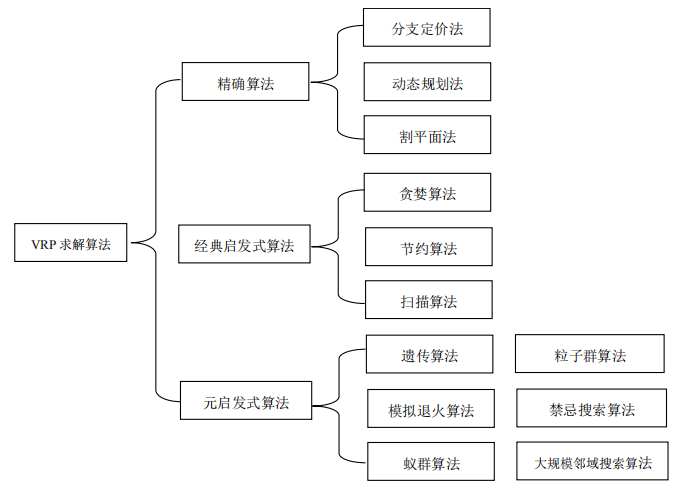
车辆路径问题作为经典旅行商问题的拓展，是一个 NP-Hard 问题，特别是对于一些约束复杂和规模较大的算例来说，想要找到最优解或近似最优解非常困难，因此车辆路径问题的求解一直是国内外学者研究的焦点。目前，车辆路径问题的求解算法可以分为以下几类：精确算法（Exact Algorithm）、传统启发式算法（Heuristic Algorithm）、元启发式算法（Metaheuristic Algorithm）。

精确算法指能求得优化问题最优解的算法，目前广泛应用于 VRP 问题求解中的精确算法包括：分支定价法（Branch and Pricing Algorithm）、动态规划法（ Dynamic Programming Algorithm）、割平面 法（Cutting Planes Algorithm）等。但是精确算法会受模型约束和求解规模的限制，一般只能求解较小规模的算例，VRP 问题已被证明是 NP-Hard 问题，随着顾客节点数量的增加，求解路径的备选方案会呈现指数性的爆炸式增长，使用精确算法往往需要巨大的时间进行求解，甚至无法求出最优解。

启发式算法起源于仿生学，是指通过对过去经验的归纳推理以及实验分析来解决问题的方法，即借助于某种直观判断或试探的方法，以求得问题的次优解或以一定的概率求其最优解。启发式算法的优劣主要是通过算法的通用性、稳定性以及收敛性来进行评判的。启发式算法可分为传统启发式算法和元启发式算法。传统启发式算法包括构造型方法、局部搜索算法、松弛方法、解空间缩减算法等。常见用于求解车辆路径问题的传统启发式算法有：贪婪算法（Greedy Algorithm）、扫描算法（Scanning Algorithm）、节约算法（Clark and Wright Saving Algorithm）等。

元启发式算法是对传统启发式算法的改进，同时结合了随机构造算法与局部搜索算法的特点，比传统启发式算法的求解更精确更稳定，而且元启发式算法往往不需要依赖于某一类问题的特定条件或情形就能够实现，因此能够用于求解不同背景、不同类型的优化问题。常用的元启发式算法包括遗传算法（Genetic Algorithm, GA）、模拟退火算法（Simulated Annealing, SA）、蚁群算法（Ant Colony Optimization, ACO）、粒子群算法（Particle SwarmOptimization, PSO）、禁忌搜索算法（Tabu Search, TS）、大规模邻域搜索算法（Large Neighborhood Search, LNS）等。

#2、自适应大规模邻域搜索算法简介

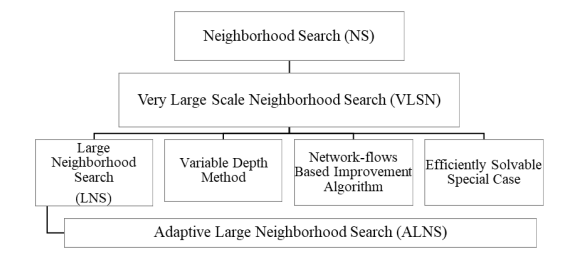
自适应大邻域搜索算法是由 Ropke 与 Pisinger在 2006 年在大规模邻域搜索算法（Large Neighborhood Search, LNS）算法的基础上提出的一种元启发式算法，其在传统邻域搜索（Neighborhood Search, NS）的基础上增加了的对算子表现的评价标准，使算法能够根据算子的表现自动选择较优的算子对当前解进行破坏与修复，从而有一定几率得到更好的解。邻域搜索算法（NS）也叫做局部搜索算法，是一类广泛应用于组合优化问题求解中的启发式算法，其原理是通过在每次迭代时对当前解执行所定义的邻域动作（Neighborhood Move），搜索当前解的邻域空间，以找到比当前解更优的可行解解，其中邻域动作就是关于当前解的一个函数，通过对当前解执行这个函数，就可以得到一个解的集合，这个解的集合就是当前解在此邻域动作下可搜索到的邻域（Neighborhood）。邻域的定义（也就是邻域动作的确定）是邻域搜索算法中最为关键的环节，一般来说可搜索到的邻域越大，每次迭代所得到的新的局部最优解的质量就越高，这样最终获得的全局最优解的质量也就越高。

在传统的邻域搜索算法中，大部分算法都只使用了一种邻域动作，比如模拟退火算法，包括 LNS 中也只使用了一种破坏算子和修复算子，因此这些算法只能搜索解空间中的很小一部分，较难找到全局的最优解；也有一些算法中使用了多种邻域动作，如变邻域搜索算法（Variable Neighborhood Search, VNS），它通过使用多个算子在当前解的多个邻域中寻找更优的解，能够有效提高算法在整个解空间的搜索范围，但是 VNS 在使用算子时会盲目地将每个算子对应的邻域动作全部执行一遍，搜索的效率并不高，缺乏一些启发式的信息指导。而ALNS 很好的弥补了上述算法缺陷：首先，ALNS 在 LNS 的基础上，允许在同一个搜索中使用多个破坏算子和移除算子来获得当前解的邻域，大大地拓展了算法的搜索空间；另外，ALNS 会为每破坏算子和修复算子分配一个权重，通过该权重来控制每个破坏算子和修复算子在搜索期间被选择的概率，并且会在迭代中动态地调整该权重，通过算子间的相互竞争来生成当前解的邻域结构，从而有很大概率能够找到更好的解。

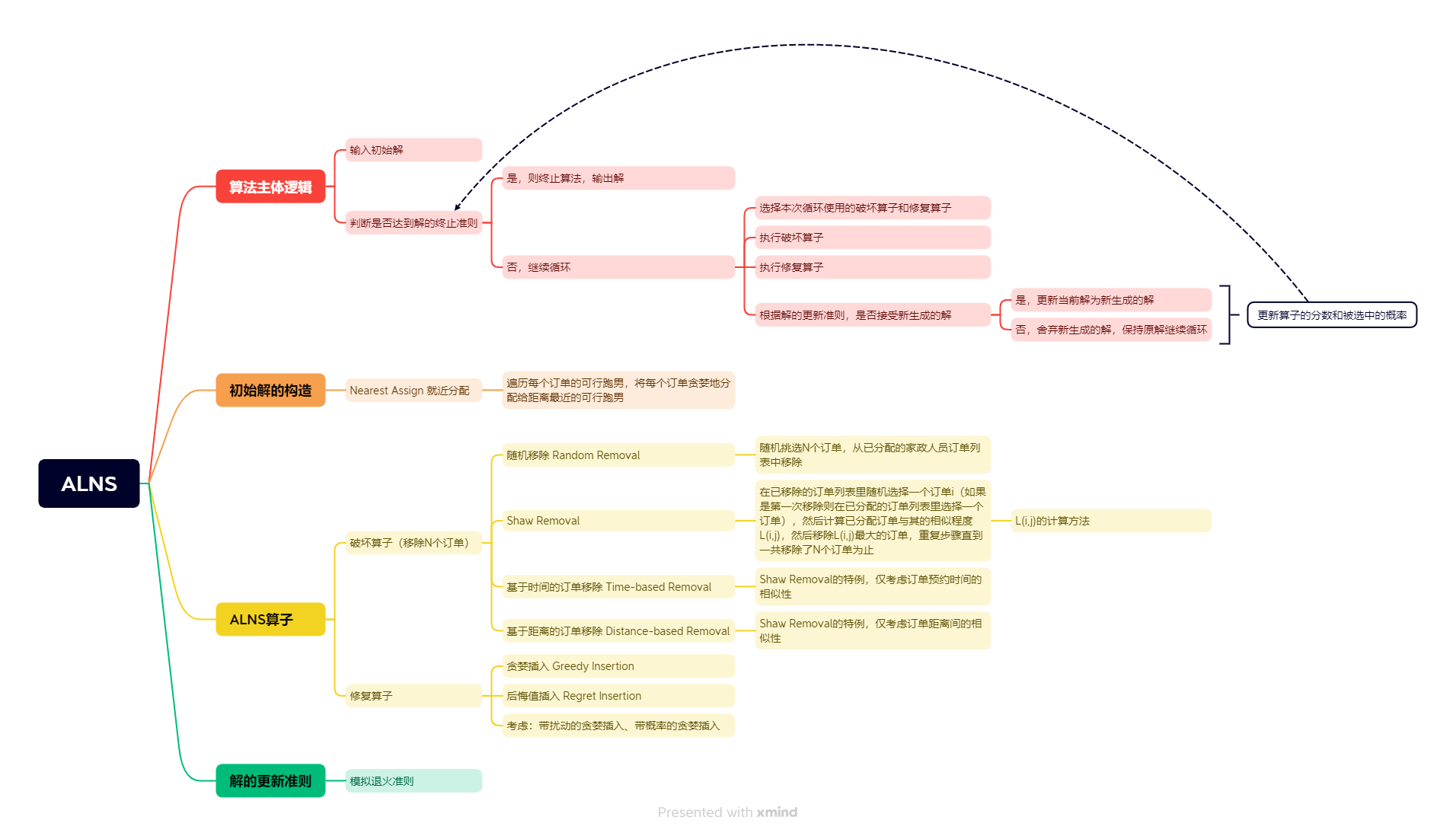
#3、ALNS算法求解派单问题

如上文所述，我们把家政派单问题抽象为一种VRPTW问题后，就很容易使用ALNS算法来进行求解了，整个过程可以描述为：

首先，使用某种规则将所有订单分配给跑男（需满足所有约束），构成派单问题的一个初始可行解(Initial Feasible Solution)；

随后，我们进行反复的循环，在每次循环中执行一种破坏算子（Destroy Operator）和修复算子（Repair Operator），简单来说，破坏算子就是把已分配的部分订单重新移除所在跑男的已分配订单列表（即所在路径），修复算子就是把移除的这部分订单通过某些准则进行重新分配，从而获得了输入解的邻域空间中一个新的可行解，这个新的解有一定概率比输入的解更优，这就是邻域搜索的过程；

每一次循环完成之后，我们会设定一个解的接受准则（Accept Criteria），如果新解比输入解更优，甚至得到了当前的全局最优解，那我们就接受这个新的解，并将其作为下一次循环的输入，如果新解比输入解更差，则需要根据接受准则进行判断，是接受还是舍弃，如果舍弃，则在下次循环中仍然使用本次循环的输入解；同时根据新解的质量，更新本次循环中使用的破坏算子和修复算子的得分，得分高的算子在之后的循环中被选择机制（Select Scheme）选中的概率也会增加，这就是算法名中自适应（Adaptive）的原理；

最后，在循环达到算法的终止准则（Stop Criteria）（通常是循环若干次或者连续若干次都没有得到改进的解）之后，停止所有算法循环，将当前的全局最优解作为算法的最终解输出。

结合UU家政的业务逻辑，我们设计家政派单的ALNS算法框架如下：

以包含50个订单、300个跑男的算例对算法效果进行测试，如图所示，相对于使用就近分配（Nearest Assign）方法生成的初始解，ALNS算法在循环达到1000次时解的改进程度达到了27%左右（事实上，由于我们的优化目标中距离的权重设置地比较高，因此当订单数量较少时，就近分配生成的初始解已经是质量较好的可行解了），而从图中我们也可以清晰看出ALNS算法通过不断循环寻找最优解的过程。

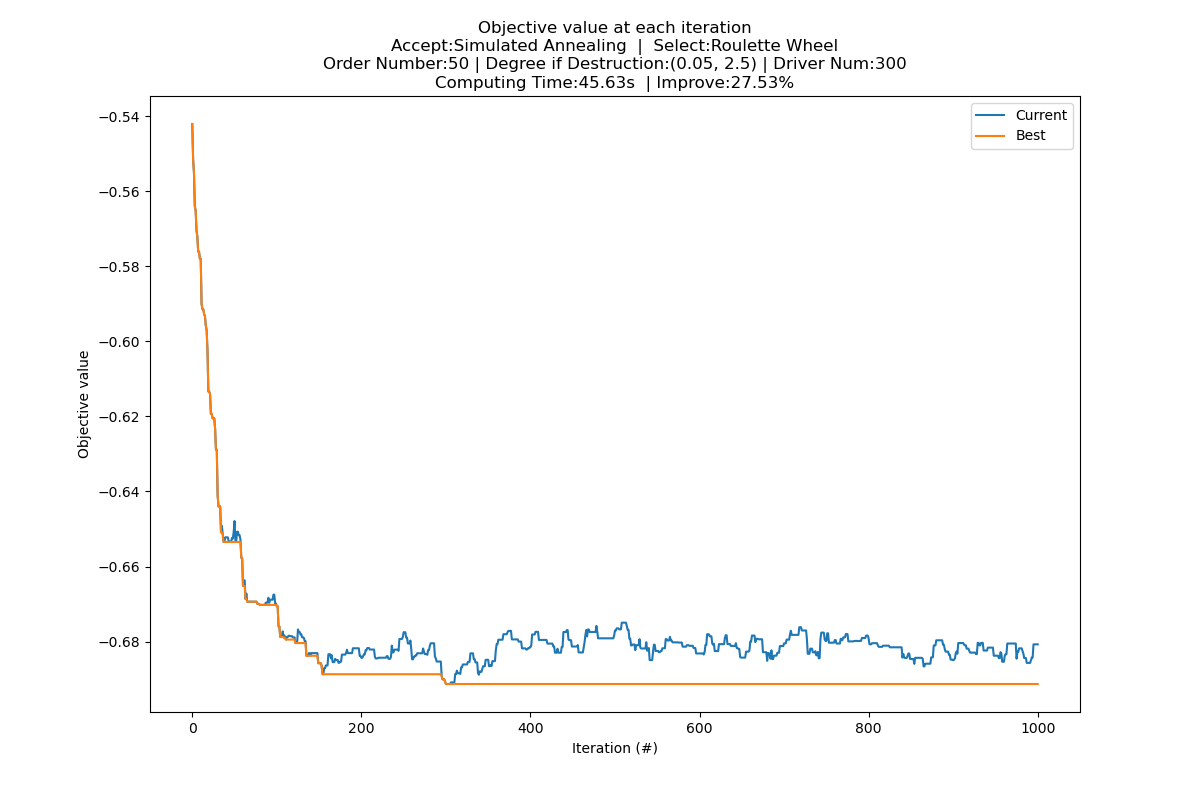
而使用ALNS算法求解家政派单问题也存在着一些不足，其中最大的问题就是算法的时间复杂度较高：目前大多数ALNS算法都会使用贪婪插入（Greedy Insertion）和遗憾值插入（Regret Insertion）作为修复算子，而我们对破坏解进行修复的过程需要遍历所有未分配订单的所有可插入位置，将最小插入成本（或者是遗憾值）最低的未分配订单分配到其最小插入成本对应的位置，这个过程的时间复杂度为O(2^n)；另外，我们在搜索每个订单的可插入位置时，也需要遍历所有的跑男，以及跑男订单列表中的每一个位置，这个过程的时间复杂度也是O(2^n)。也就是说当算例中包含的订单（在我们的问题中还包括跑男身上原有的订单）和跑男数量级持续增长时，整个算法的求解时间会相应地呈现指数级增长，这可能会造成订单响应的延迟。当然，对于当前家政订单的体量而言，ALNS算法是能够在可接受的时间内得到可行解的，未来需要从数据结构优化和修复算子优化这两个方向对算法的时间复杂度进行改进。另外，当前的自适应准则只是单纯通过简单的分数加减来评判各类算子的优劣，从而决定接下来被选中的概率，这种自适应准则具有一定的局限性，当前已有部分研究将机器/强化学习算法加入算子的选择机制中（当前有一些开源的项目在选择机制中加入包括多臂老虎机算法在内的机器学习算法 https://github.com/N-Wouda/ALNS），未来也可以做这方面的尝试。

#四、算法上线效果

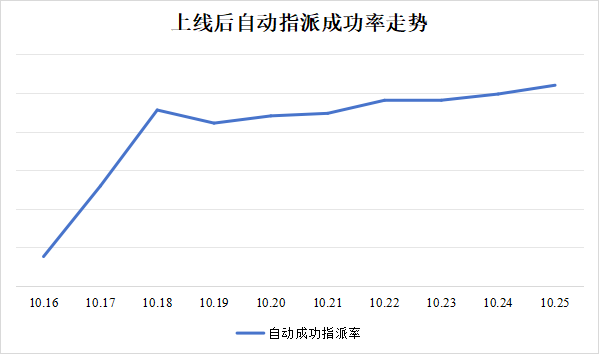
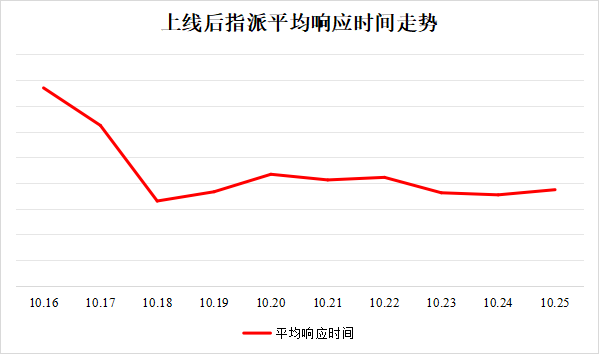
目前新版的自动派单算法已经在郑州正式上线近两周的时间，在此期间由产品经理向家政运营宣导了新的指派模式，同时根据上线后的数据进行了相应的参数调整和优化，结果显示，相较于原有的自动指派逻辑，新版自动派单+唤醒算法上线后的自动指派成功率提升了2倍以上，订单的平均响应速度也得到了明显缩短，算法在短期内效果基本符合预期。

#参考文献

[1] Ropke S, Pisinger D. An adaptive large neighborhood search heuristic for the pickup and delivery problem with time windows[J]. Transportation Science, 2006, 40(4):455-472. https://doi.org/10.1016/j.cor.2016.01.018

[2] Shaw P. Using constraint programming and local search methods to solve vehicle routing problems[J], International Conference on Principles and Practice of Constraint Programming, 1998, 1520:417-431. https://doi.org/10.1007/3-540-49481-2_30

[3] Schneider M, Stenger A, Goeke D. The Electric Vehicle-Routing Problem with Time Windows and Recharging Stations[J]. Transportation Science, 2014, 48(4):500-520. https://doi.org/10.1287/trsc.2013.0490

[4] Solomon M M. Algorithms for the Vehicle Routing Problem with Time Windows[J]. Transportation Science, 1995, 29(2):156-166. http://dx.doi.org/10.1287/opre.35.2.254

[5] https://blog.csdn.net/qq_58446570/article/details/128684643

[6] https://github.com/N-Wouda/ALNS