前言

     随着智能手机和无线网络的普及，时空众包平台(Spatiotemporal Crowdsourcing)的兴起如图1，极大的改变了人们的生活方式，使我们的生活更加便捷。诸如此类的时空众包平台具有类似的特点，这些平台以时空数据管理平台为基础，将具有时空特性的众包任务分配给非特定的众包参与者群体为核心操作，并要求众包参与者以主动或被动的方式来完成众包任务并满足任务所指定时空约束条件的一种新型众包计算模式。 

图 1 国内外时空众包应用

     在时空众包平台中，越来越来的在线Ridesharing平台开始出现在我们的视野里，在及时配送领域常见的有UU跑腿，闪送、达达、顺风同城、饿了么和美团蜂鸟等，在交通运输领域如滴滴、Uber和Lyft等。 Ridesharing平台在运营过程中都会面临着一些相同的问题，例如如何使需求方可以获取到更加好的体验，如何在时空的基础上对供需双方进行匹配、如何对供方进行运力分布进行均衡调度等。有三大典型的市场干预手段：自动派单（Matching）、运力调度（Repositioning）和定价（Pricing）。自动派单和运力调度直接涉及到运力分布，而定价则可以对供需双方分布进行调节。在之前的文章（https://tech.uupt.com/?p=480 ）里我们对自动派单进行简单的介绍，以及在我们工作中的实践和应用。本文将对运力调度技术的调研成果进行初步介绍，为下一步在工作中运力调度的应用打下一个坚实基础。

问题介绍

      在城市的发展过程中，为了实现城市功能的空间集聚形式，往往会出现不同的功能区，产业集聚和功能优化是城市功能区的本质特征。例如在早上上班的高峰期，很多上班族具有从居民区到办公地的出行需求，车辆源源不断的从居民区到办公集聚区，导致运力在办公地越来越聚集，而居民区的运力不足，导致有出行需求的人越来越难打到车。例如及时配送行业，在520或者节假日的时候，花卉市场或者商业区的订单量激增，运力分布不均衡导致这些区域的订单取消率居高不下。

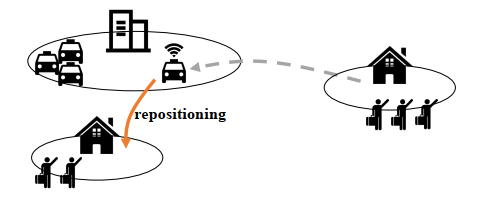
图 2 供需不平衡的产生

      运力调度就是为了解决运力和需求不平衡的问题。在实践过程中，当司机或者跑男师傅们空闲的时候，有一部分师傅往往会根据自己的经验，前往他们认为接单概率大的地方去，这其实就是一种最初级最原始的基于自我驱动型的运力调度。自我驱动型的运力调度和抢单的弊端类似，都是师傅们站在自我利益最大化的角度最出的决策行为，这样的行为从全局来看效率低下，甚至会影响双方的体验。与自我驱动型相对的是全局驱动型，全局驱动型运力调度与自我驱动型运力调度相比存在一个突出的优势是全局驱动型运力调度是站在一个全局更高的维度进行规划和决策的，产生的效益也比自动驱动型调度更高。我们来看图3的一个场景，图中六变形的颜色深浅表示需求量，颜色越深，对运力的需求量越大，如果基于自我驱动型的运力调度，周边的4个运力根据他们的经验，需求量最大的区域对他们来说具有更高的吸引力，而实际是颜色最深的区域只需要2个运力就可以满足需要。如果是基于全局驱动型的运力调度，则会把另外2个运力分别调度到颜色次深的区域以便于运力分布更加均衡化。

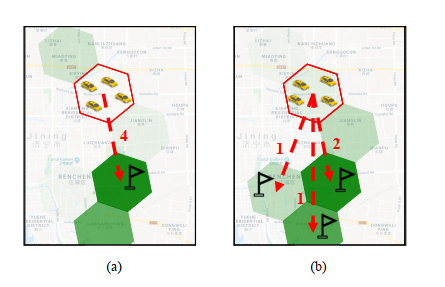
图 3 自我驱动型(a)和全局驱动型(b)的运力调度

解决思路

       基于以上描述的问题，本文详细说明两种解决思路，分别是运筹优化和强化学习两种方法。

       运筹优化方法的总体思路是：基于经济学建模与运筹优化思路的运力调度方案，核心在于维护一个供需率与响应率的分段线性函数，然后度量每个网格增加一个跑男的边缘增益，采用最优化的思想，获得一个当全局增益最大时的运力调度方案。其中涉及到两个机器学习（包括深度学习）子模型：Task的接受概率和订单需求的预测。通过做ab试验，消融性研究等验证了模型的有效性 。

       强化学习方法的总体思路是：每个车辆有7中可能的调度结果，调度到6个近邻的六边形网格中或是待在当前网格中，采用两个上下文多agent算法：cA2C和cDQN。

运筹优化

       Task由构成合适的师傅、目的地、过期时间和激励（可选）四个部分构成，每一个Task就是一个调度任务，如果师傅接受了一个调度任务，当他前往目的地的路上或者到达目的地一段时间内收到了一个需求，则认为调度成功；当师傅接受了调度任务，在规定的时间内到达目的地，等待一定得时间没有获取到一个需求，则认为调度失败。这是对调度成功失败的定义。整个过程分为生成候选的Task、对Task进行评分和规划求最优解三个过程 。

（1）生成候选的Task

       生成候选的Taks时，通常选择那个空驶超过一定时间或是抢单失败超过一定次数的师傅。目的地需要根据选择的师傅来选择，通常是师傅当时位置所在网格的相邻网格或者次相邻网格。也可以对师傅的历史轨迹进行数据挖掘挑选一些合适的网格。过期时间则由ETA模块进行预估。

（2）对Task进行评分

        对每个Task进行评分，这里采用调度1个师傅前往相应的网格，该网格订单响应率的提升幅度来作为评分标准，具体做法是需要拟合一个供需率与订单响应率的分段函数，如图4所示，y轴为响应率Rr = 响应订单/发单量，x轴为供需率为运力数量与订单数量之比，即 |D| / |O|。

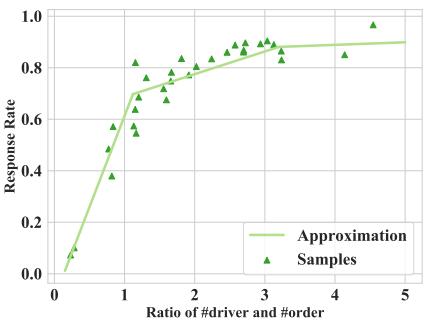
图4 订单响应率和供需关系

       根据历史数据通过拟合得到的订单响应率和供需关系函数如公式（1），用U(rep)表示对公式（1）求|D|的导数得到公式2，U(rep)的意义表示每增加1个运力，订单响应率的提升幅度，其中表示未来t时刻，网格g的预测订单量。我们便可以用U(rep)来作为Task的评分。

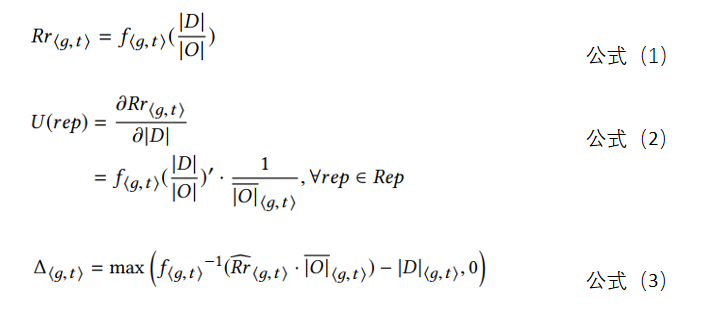
     通过历史数据拟合得到的订单响应率和供需关系分段函数公式（1），我们还可以获取到一个有意义的结果，通过设置一个网格未来某时刻的订单响应率，再结合该网格未来某时刻的预计订单量，我们可以计算出如果保证设置的订单响应率的前提下，需要多少位跑男师傅，然后与当前网格的跑男师傅数量之差就是需要调度到该网格的跑男数量。我们在规划求最优解的时候可以作为一个模型的约束。

（3）规划求最优解

      在这小节，我们可以设置一个全局目标：最终Task的总得分最大。其中涉及到两个约束，约束一是为了控制每个跑男最多只能有一个调度任务，约束二是我们可以设置一个订单响应率的上线，控制前往一个网格的跑男数量不会超过达到设置订单响应率所需跑男的最大数量。

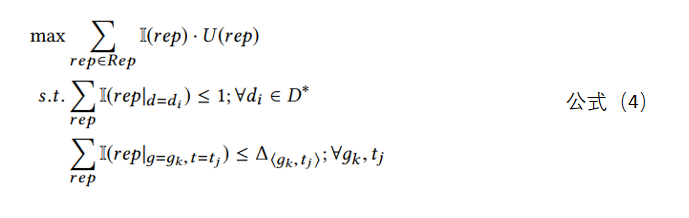
      上传最优化模型是一个线性0-1整数规划，需要一定的计算量，为了简便期间，我们可以把这样一个最优化化模型转换为图论中的最小代价最大流问题。如图5所示，每条边的标签为 ⟨θ,w⟩，θ表示边的容量，w表示代价。如此以来，问题就变成了求解经典的最小代价最大流问题，如果求解器都具备这样的功能。

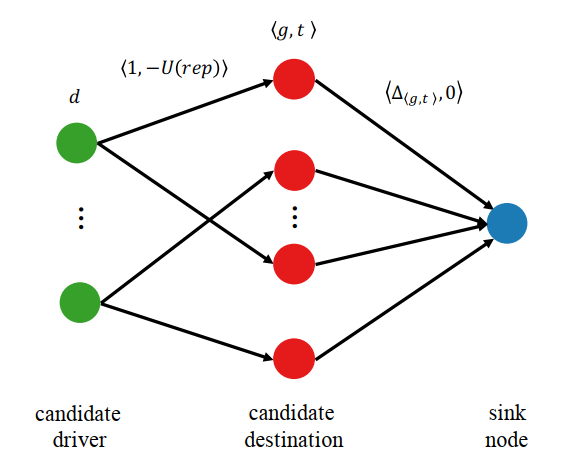
图5 最小代价最大流模型（边的标签分别表示容量和代价）

总结

     这样一个最优化模式是一个经典的处理方法，模型透明，具有解释性。首先根据历史数据拟合得到一个函数，量化调度一个跑男到相应的网格对订单响应率的贡献，再站在全局的角度上求一个订单响应率最大提升的调度方案，我认为只有以下几点可以限制或需要优化的地方：

     （1）根据历史拟合出来的订单响应率和供需关系函数是决定模型是否能产生好的效果的关键。实际过程中每个六边形网格不是相互独立的，其订单响应和供需在网格之间相互影响，获取一个准确的函数是一件具有挑战的事情。

     （2）公式3在计算未来某个时刻所需要的跑男数量时，默认当前网格的跑男数量和未来的跑男数量一致的，实际过程中，跑男数量和位置是动态变化的，可能导致计算出来的数据不准确，可以采用未来该时空跑男的预计数量作为参考，这一点是一个优化方向。

     （3）当把一个Task分发给一个运力时，因为是非强制性调度，运力具有一定的拒绝概率，这就造成了规划处理的结果是全局最优的，但是在实施的过程因为没有按照这个最优方案来实施，从而实际的调度方案不是最优的，可以将在对Task的评分和规划求解的过程中加上失败率因素。

强化学习

（1）问题描述

Agent, State, Action

       把每个空闲的运力当作一个agent，把在同一个时间间隔同一个网格的运力当作相同的agent。在实际t，我们维护一个包含优先运力及订单分布的全局状态St，对时间和网格进行one-hot编码。我们使用六边形网格系统来表示地理信息，每个agent都有7个可以选择的action，当前所处网格的周边有6个邻接六边形，还有1种选择是保持在当前网格不动。如图6所示， ait ≜ [g0; g1]表示agent i从网格g0调度到g1。

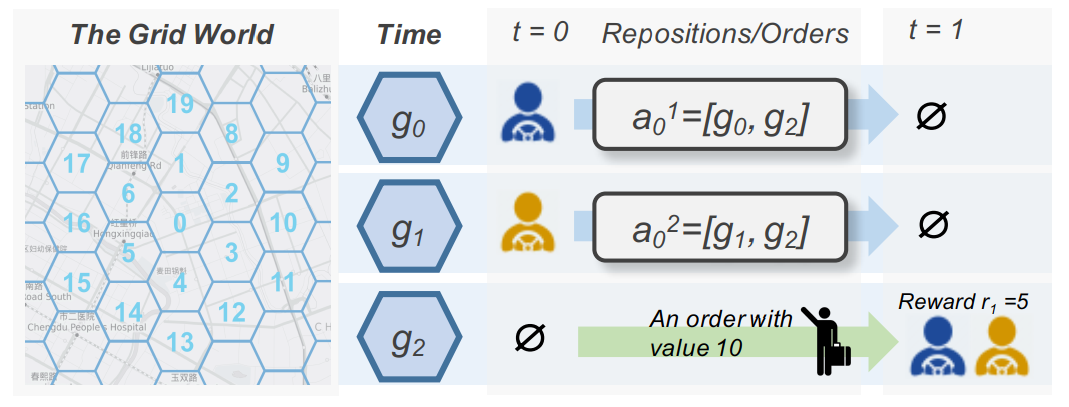
图 6 时空网格已经问题的设置可视化

Reward function, State transition probability

        每个agent都有一个奖励函数，相同网格内的所有运力的奖励函数相同，且在相同的时间内同一个网格的奖励也是相同的。 状态转移概率p(st+1 | st ;at ) : S × A × S 在0—1之间，给出了在动作at的前提下，状态从st到st+1的转移概率。

（2）上下文多Agent强化学习

        本文提出了两个上下文的多agent强化学习算法：contextual multi-agent actor-critic (cA2C)，算法2和contextual DQN (cDQN)。

参考文献

[1] http://iri.buaa.edu.cn/info/1016/1291.htm

[2] Qin, Zhiwei, Xiaocheng Tang, Yan Jiao, Fan Zhang, Zhe Xu, Hongtu Zhu, and Jieping Ye. “Ride-Hailing Order Dispatching at Didi via Reinforcement Learning.” INFORMS Journal on Applied Analytics 50, no. 5 (2020): 272–86.

[3] Xu, Zhe, Chang Men, Peng Li, Bicheng Jin, Ge Li, Yue Yang, Chunyang Liu, Ben Wang, and Xiaohu Qie. “When Recommender Systems Meet Fleet Management: Practical Study in Online Driver Repositioning System.” In Proceedings of The Web Conference 2020, 2220–29. New York, NY, USA: Association for Computing Machinery, 2020. https://doi.org/10.1145/3366423.3380287.

[4] Lin, Kaixiang, Renyu Zhao, Zhe Xu, and Jiayu Zhou. “Efficient Large-Scale Fleet Management via Multi-Agent Deep Reinforcement Learning.” ArXiv Preprint ArXiv:1802.06444, 2018.

[5] Jin, Jiarui, Ming Zhou, Weinan Zhang, Minne Li, Zilong Guo, Zhiwei Qin, Yan Jiao, et al. “Coride: Joint Order Dispatching and Fleet Management for Multi-Scale Ride-Hailing Platforms.” In Proceedings of the 28th ACM International Conference on Information and Knowledge Management, 1983–92, 2019.