一、问题简述
在生活或者生产中,有时候我们追求的不止一个目标,例如当你正在规划一次长途旅行,其中涉及到交通方式,你想追旅途舒适的同时,也希望能够省钱;当公司规划一年的预算时,希望得到一个获得经济效益最大且最少支出的方案等。这时就涉及到多目标优化问题即Multi-Objective Optimization Problems (MOOP) ,多目标问题在优化过程中涉及到多个最大化或者最小化目标,其问题的解是权衡了多个优化目标后的一组最佳解决方案。广义的多目标问题数学表达式如下:
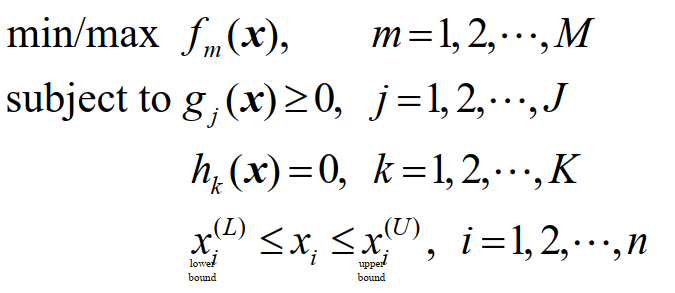
二、Pareto优化
1. 支配
多目标优化问题优化过程中涉及到一个重要的概念叫支配(Dominance )。在单目标优化问题中,解的优劣是很容易比较的,只需要判断两个解的目标函数值就可以了,但是在多目标的优化问题中,这样就行不通了,我们采用解是否被支配来确定两个解的优劣。有两个解x1和x2,如果x1支配x2则需要满足两个条件:
- 在全部的目标函数上,解x1是不会比解x2更差
- 至少在一个目标函数上,解x1要优于接解x2
当同时满足这两个条件时,我们称x1支配x2,即x2被x1支配。下面是有关支配验证的示例:
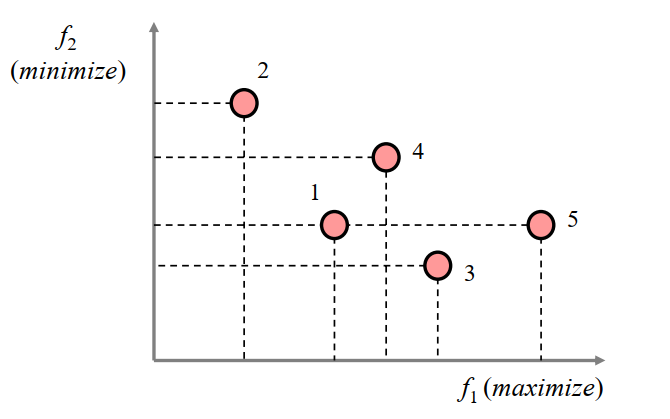
- 解1 vs 解2:解1支配解2
- 解1 vs 解5:解5支配解1
- 解1 vs 解4:两者互不支配
2. Pareto最优
我们对pareto优化过程中涉及到的核心概念进行定义和解释:
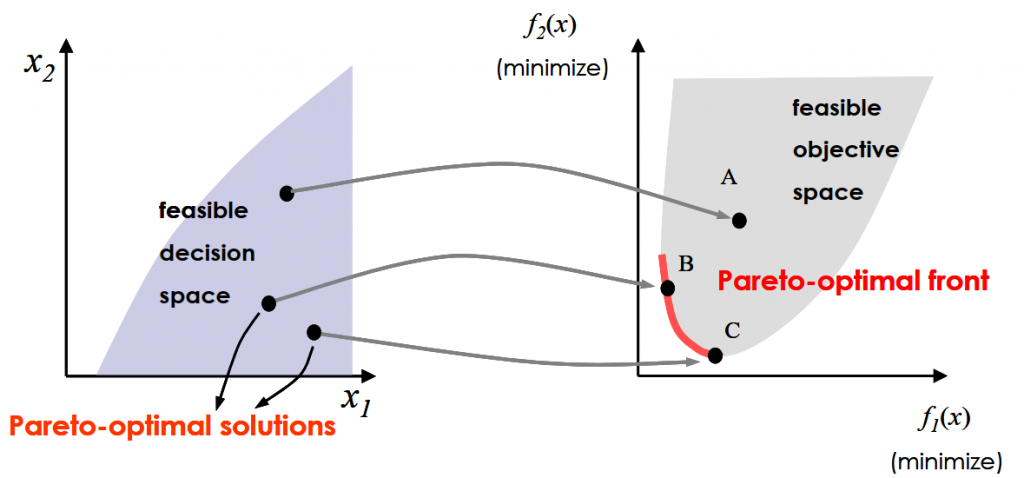
非支配解集(Non-dominated solution set ):在一个解的集合中,全部解都不会被这个解集中任意一个解支配;
pareto最优解(Pareto-optimal set ):整个决策空间中的非支配解集被称为pareto最优解;
pareto最前沿(Paretooptimal front ):全部的pareto最优解对应的目标函数的边界被称为pareto最前沿。
3. 多目标优化目标
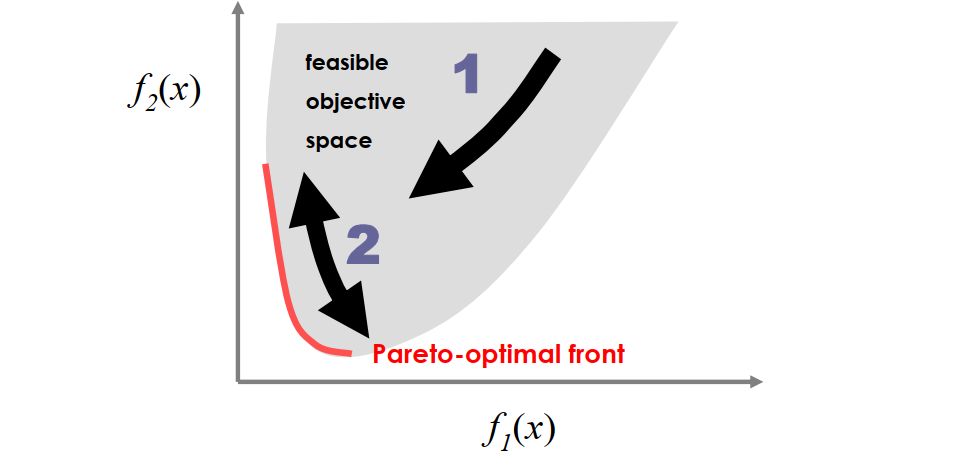
在多目标的优化过程中,我们追求两个目标:
- 找到尽可能的接近pareto-optimal front的解
- 尽可能的发现不同的解
三、求解方法
1. 传统的求解方法
- Weighted Sum Method
通过自定义每个目标的权重,权重与目标相乘,从而将多个目标转换为一个目标来求解。

优点:简单,容易实施
缺点:(1)无法设置合适的权重向量获得解空间中的Pareto-optimal
(2)针对非凸的目标空间,该方法不能得到Pareto-optimal solutions,如下图所示。

- ε-Constraint Method
选择一个目标进行优化,将其余的目标转换为指定范围内的约束,从而进行单目标优化。
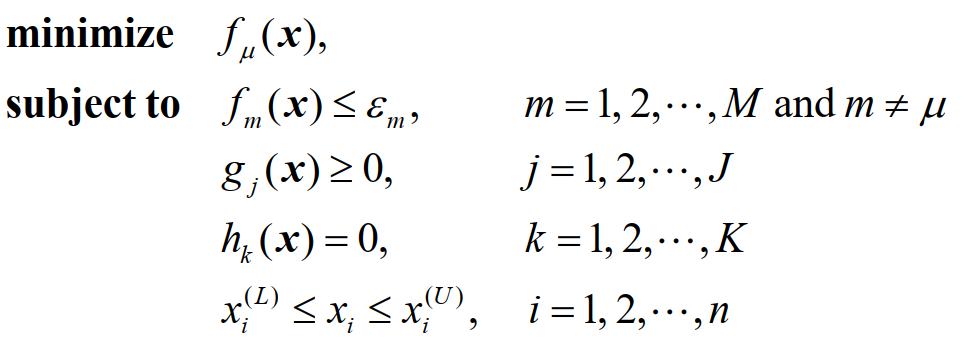
优点:可以应用于凸优化问题或者非凸优化问题
缺点:ε向量值的选择是需要注意,相当于舍弃了部分可行解空间,剩余的可行解空间需要包含优化目标的最大最小值。
- Weighted Metric Method
假设z*是一个理想的解, 采用一个权重向量,最小化目标函数与解z*的综合距离。

优点:加权的Tchebycheff metric 可以保证得到全部的Pareto-optimal solutions
缺点:(1)需要知道目标函数的最大最小值
(2)为了获得理想解z*,需要独立的优化每个目标函数
(3)对于较小的p值,不能获得全部的Pareto-optimal solutions
(4)随着p值的增加,问题将会变得不可微
2. 遗传进化算法
经典的多目标算法往往是将多个目标转为一个目标的思路来求解,遗传和进化算法相对于经典的多目标算法来说,有以下三个优势:
- 可以得到一个最优解集合
- 传统的多目标优化方法只能得到一个候选解
- 进化遗传算法基础的算子针对整个候选解集合进行优化
以下列出常见的多目标遗传算法及优劣势:
| 算法 | 多样性机制 | 精英主义 | 外部种群 | 优势 | 劣势 |
|---|---|---|---|---|---|
| VEGA | No | NO | No | 第一个简单易懂的MOGA实施 | 趋向收敛与每个目标的两极 |
| MOGA | No | No | 简单的扩展了单目标的GA | 收敛慢 | |
| WBGA | No | No | 简单的扩展了单目标的GA | 解决非凸问题困难 | |
| NPGA | No | No | 采用锦标赛选择过程 | 参数和问题相关 | |
| RWGA | 随机对权重进行分配 | Yes | Yes | 有效率且容易实施 | 解决非凸问题困难 |
| PESA | Pure elitist | Yes | 容易实施且计算效率高 | 性能取决于单元数,需要关于目标空间的先验知识 | |
| PAES | Yes | Yes | 随机变异登山策略 | 不是一个基于种群的方法 | |
| NSGA | No | No | 计算效率高,容易收敛 | 性能取决于单元数 | |
| NSGA-II | 拥挤度距离 | Yes | No | 单个参数,方便测试,高效 | 问题和参数有关系 |
| SPEA | Yes | Yes | 方便测试,无参数聚类 | 拥挤度距离只能再目标空间起作用 | |
| SPEA-2 | 基于knn的密度距离 | Yes | Yes | SPEA提升版,确保极端点被保留 | 复杂的聚类算法 |
| RDGA | Yes | Yes | 动态单元更新,目标数量方便是健壮的 | 计算代价高 | |
| DMOEA | Yes(implicitly) | No | 包含高效的计算去更新单元密度,参数自适应 | 实施困难 |
参考文献
[1]https://engineering.purdue.edu/~sudhoff/ee630/Lecture09.pdf
[2]Konak, Abdullah, David W. Coit, and Alice E. Smith. “Multi-Objective Optimization Using Genetic Algorithms: A Tutorial.” Reliability Engineering & System Safety, Special Issue – Genetic Algorithms and Reliability, 91, no. 9 (September 1, 2006): 992–1007. https://doi.org/10.1016/j.ress.2005.11.018.
[3]Marler, R.T., and J.S. Arora. “Survey of Multi-Objective Optimization Methods for Engineering.” Structural and Multidisciplinary Optimization 26, no. 6 (April 1, 2004): 369–95. https://doi.org/10.1007/s00158-003-0368-6.
[4]Deb, Kalyanmoy. “Multi-Objective Optimisation Using Evolutionary Algorithms: An Introduction.” In Multi-Objective Evolutionary Optimisation for Product Design and Manufacturing, edited by Lihui Wang, Amos H. C. Ng, and Kalyanmoy Deb, 3–34. London: Springer, 2011. https://doi.org/10.1007/978-0-85729-652-8_1.
