背景
(2)自动派单是公司发展到一定规模时必然出现的一个产物。在初期由于规模小,过程和技术简单的抢单模式更容易受到青睐。随着公司业务规模的发展,城市的订单量迎来大幅度增长,跑男抢单与客服指派相结合的模式已经不能满足业务的需求,甚至会制约公司的发展。跑男抢单时,需要在较短的时间内来判断是否顺路,是否可以接单等,对跑男的要求比较高且效率低下,并且在订单充裕的情况下,存在严重的挑单行为,造成一部分用户或商户的订单不能被服务,运力得不到充分的利用。除此之外,在母亲节、情人节等订单高峰期订单积压的时候,对指派订单的客服来说是一个不小的挑战。
目的与意义
- 充分利用运力,提升订单消化能力,降低订单取消率;
- 简化跑男接单流程,提高跑男接单效率和人效;
- 从接单时长、取货距离、取送货超时等多个方面提升用户服务体验;
- 减轻订单高峰期客服人员派单压力;
- 减少公司对核心跑男的依赖程度,提高对跑男的把控力度。
问题调研
我们的派单问题本质上是一个订单取送问题,即Pickup and delivery problem(PDP)是VRP的一个变种,主要解决车辆把物品和乘客从起点转运到目的地的行驶路径规划问题,如图1所示。vehicle routing problem (VRP)是一个组合优化问题,一个整数规划问题,主要解决车辆往客户点转运物品的行驶路径规划问题。

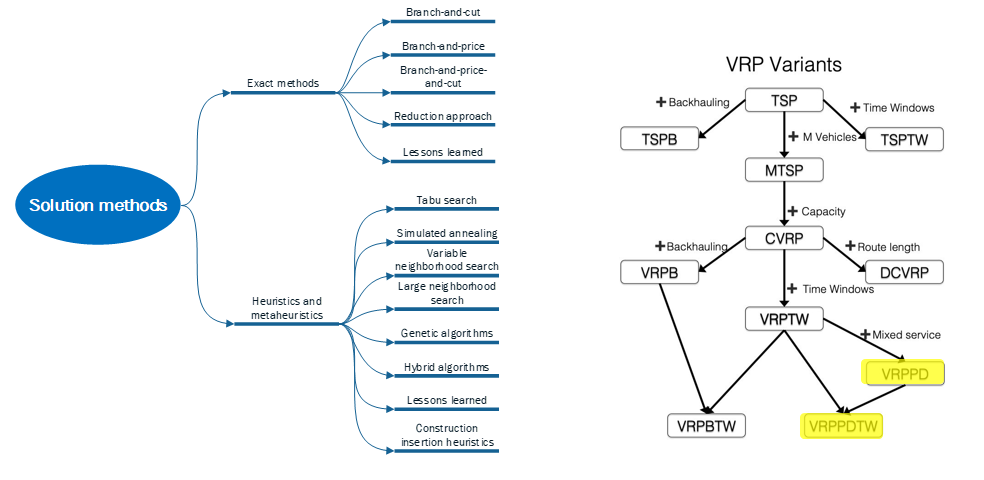
求解PDP的算法大概可以分为两类:启发式算法和精确算法,如图2(左)所示。精确算法如Branch-and-cut、Branch-and-price、Branch-and-price-and-cut等可以获取一个最优解,通常适用于小规模问题,而大规模问题多采用启发式算法如ALNS、Tubu search 、Simulated annealing、VNS、LNS等,启发式算法往往是在有限的时间内获得一个相对优的解。
方案调研
1.饿了么
方案 1:模拟退火算法解决车辆路径规划
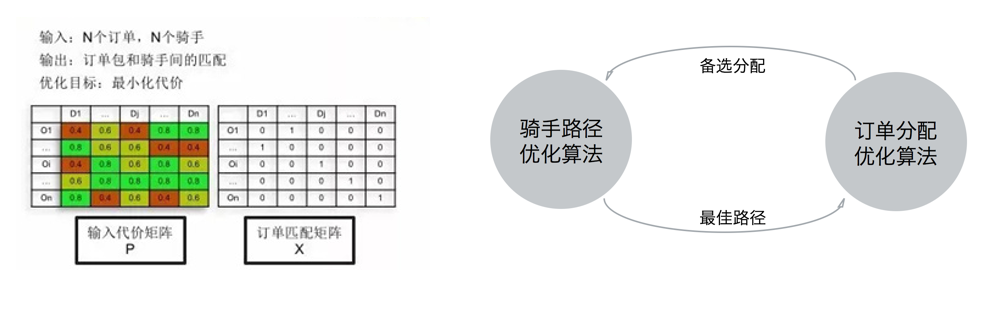
方案2:先计算最优代价矩阵,基于大量函数的组合算法,核心算法KM最优匹配,如图3(左)所示。
2.美团
• 问题特征分析:针对配送调度的场景,这个问题可以被分解为两个层次:骑手路径优化和订单分配方案的优化,如图3(右)所示。骑手路径优化问题要解决的问题是:在新订单分配至骑手后,确定骑手的最佳配送线路;而订单分配优化问题要解决的问题是:把一批订单分配至相应的骑手,使得我们关注的指标(如配送时长、准时率、骑手的行驶距离等)达到最优。这两个问题的关系是:通过订单分配优化算法进行初始的订单分配,然后通过骑手路径优化算法获取各骑手的最佳行驶路线,进而,订单分配优化算法根据骑手路径优化结果调整分配方案。这两个层次不断反复迭代,最终获得比较满意的解。
• 跨学科结合:订单分配问题在业内有两类方法,第一类方法是把订单分配问题转换成图论中的二分图匹配问题来解决。但是由于标准的二分图匹配问题中,一个人只能被分配一项任务,所以常用的一个方法是先对订单进行打包,将可以由一个人完成的多个订单组成一个任务,再使用二分图匹配算法(匈牙利算法、KM 算法)来解决。
3.滴滴
•批量匹配(全局最优):这个算法几乎是所有类似派单系统为了解决这个问题的最基础模型,在Uber叫做Batching Matching,我们内部也叫做“全局最优” 或者 “延迟集中分单”。找寻司机和订单分配的全局最优是一个 二分图匹配问题 (bipartite graph matching) ,一边是乘客、一边是司机,可用运筹优化中各种解决Matching问题的方法进行求解。
•基于供需预测的分单:利用对未来的预测,即进行基于供需预测的分单。
•连环派单:基于供需预测的分单有很大意义,但由于预测的不确定性,其实际效果很难得到保证。为此,我们使用了一种更有确定性的预测方式来进行派单,即 连环派单。环派单预测的是下一时刻空闲司机的所在位置。由于高峰期空闲司机多为司机完成订单后转换而来,预测司机的位置就变成了一个相对确定性的问题,即监测司机到目的地的距离和时间。当服务中的司机距终点很近,且终点离乘客新产生的订单也很近时,便会命中连环派单逻辑。
算法架构
从全局最优考虑的派单算法的核心是在维护一个最小代价增量矩阵,如图5(右)所示,然后从这个矩阵中计算出最小代价的最大匹配。计算最小代价增量矩阵的就需要解决两个主要问题:代价矩阵是如何构成的和计算订单和跑男的最优行驶路径。派单算法架构如图4所示。

(1)代价矩阵是如何构成。代价需要根据公司运营过程中所追求的目标来进行构建,我们公司的主要业务是订单的取送,在订单的取送过程中涉及到到三类对象:发货人、跑男和收货人。我们以时间作为考量,分别用发货人的取件时长、跑男的工作时长和收货人的收货时长来衡量对三者的服务质量,如图4(左)所示。当出现一个新订单时,假设分派给跑男以后,发件人身上所有需要取件订单的取件时间之和越短、跑男的总工作时间越短和所有订单的收货时长之和越短三者的体验越好,然后可以将三者归一化以后加权并求和。
(2)计算订单和跑男的最优行驶路径。确定了总体的代价构成,我们需要计算跑男分配订单前后的总工作时长、取件时长之和、送件时长。跑男行驶路径不同,导致的时长也会不同。通常跑男在行驶时,是按照时间最短的行驶方案进行配送物品,我们需要计算跑男分配订单前后的最优行驶路径。这个问题在运筹学上属于小规模的车辆路径规划中的PDPTW,我们采用动态规划的思想进行求解,支持预约单和软时间窗等。

假设当前有n个新订单需要进行指派,有m个跑男可以进行派单,如果不进行过滤的话会需要计算n x m个最优行驶路径问题,需要消耗巨大的算力。通常在这个矩阵中有的新订单和跑男是不会产生联系的,也就没必要计算这个跑男接这个新订单之后代价增量,例如新订单的取货位置距离跑男超过10km的,或者根据业务逻辑没有带保温箱的跑男不能接美食订单等。
基于以上的考虑,算法中设置了前置过滤器和后置过滤器。经过前置过滤器被过滤掉的<订单-跑男>副不再进行订单和跑男的最优行驶路径规划,后置过滤器的指经过了订单和跑男的最优行驶路径规划,但是仍有不满足一些要求的<订单-跑男>副会再次被过滤掉。例如经过订单和跑男的最优行驶路径规划,跑男接这个新订单肯定会造成身上的订单超时,我们就不能再给这个跑男派新订单了。整个算法的计算瓶颈在于<订单-跑男>的最优行驶路径规划,前置过滤器的设置可以大幅度减轻该环节的计算压力。
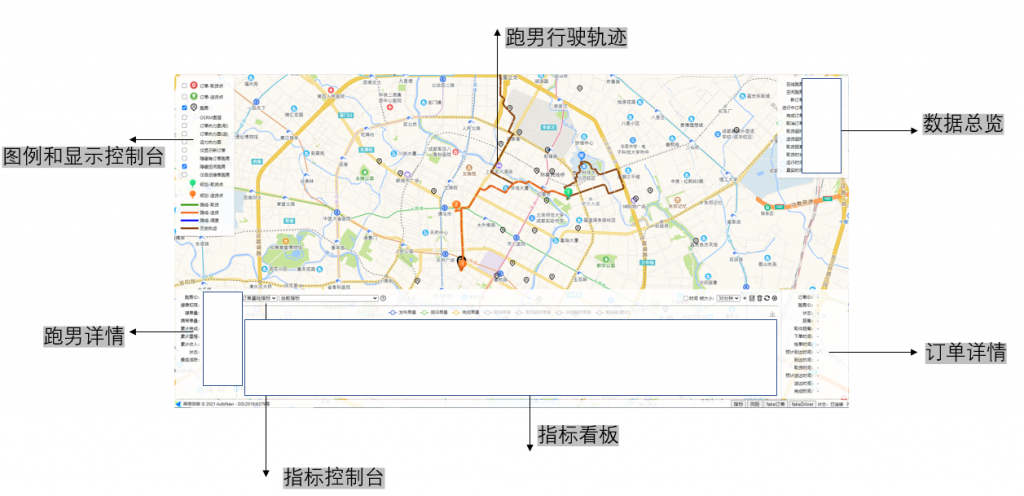
经过上述两个过程的计算,我们可以得到一个最小代价增量矩阵,如图5(右)所示,通过KM算法计算出来一个最大匹配的最小代价指派。我们便可以获得到新订单的指派方案。为了保证算法的质量,还需要对算法进行验证。我们开发了相应的算法模拟器、实时分析系统和派单日志更新系统等,如图6所示。
持续优化
1)算法参数自适应:算法参数自适应场景,例如在订单少的时候,侧重用户体验;在订单充足的时候,侧重订单相应率。
2)提高首单派单权重:在派单过程中,优先对用户首单进行派送。
3)取货时间和出货时间预估:当前智能派单算法中的取货时间和出货时间是一个固定值,未来规划将对其进行预估,以满足不同门店不同时段等情况的动态调整。
4)运力分布均衡化引导:派单系统需要结合运力引导才能发挥最大的作用,未来需要基于全局最优的思想,对运力分布进行均衡化引导,进一步降低订单取消率。
参考文献
[1] https://en.wikipedia.org/wiki/Vehicle_routing_problem
[2] Berbeglia, Gerardo, J. Cordeau, and G. Laporte. “Dynamic Pickup and Delivery Problems.” Eur. J. Oper. Res. 202 (2010): 8–15.
[3] Ho, Sin C, W. Y Szeto, Yong Hong Kuo, Janny M. Y Leung, Matthew Petering, and Terence W. H Tou. “A Survey of Dial-a-Ride Problems: Literature Review and Recent Developments.” Transportation Research Part B Methodological 111, no. MAY (2018): 395–421.
[4] https://cloud.tencent.com/developer/article/1007286
[5] https://tech.meituan.com/2017/10/11/o2o-intelligent-distribution.html
[6] https://mp.weixin.qq.com/s/0X7gFioC3N-B6qbZ7qqsaA
[7] Gendreau, Michel, Jean-Yves Potvin, and others. Handbook of Metaheuristics. Vol. 2. Springer, 2010.
[8] Pisinger, David, and Stefan Ropke. “A General Heuristic for Vehicle Routing Problems.” Computers & Operations Research 34, no. 8 (2007): 2403–35.
[9] Ropke, Stefan, and David Pisinger. “An Adaptive Large Neighborhood Search Heuristic for the Pickup and Delivery Problem with Time Windows.” Transportation Science 40, no. 4 (2006): 455–72.
[10] Krol, Emiel, and Niels Wouda. “OR Analysis of Complex Systems,” March 2020. https://github.com/N-Wouda/OR-Analysis.
[11] Burkard, Rainer, Mauro Dell’Amico, and Silvano Martello. Assignment Problems. Other Titles in Applied Mathematics. Society for Industrial and Applied Mathematics, 2012. https://doi.org/10.1137/1.9781611972238.
