最近UU前端团队内部兴起了新一波技术迭代,学习的风潮,很多同学在尝试利用新的技术栈去重构旧的项目,其中就有很多同学重写了九宫格拼图游戏,有些利用vue3+vite重构游戏组件,有些利用canvas重新实现了游戏逻辑,身为前端组一员,这种活动怎能错过,于是另辟捷径,为九宫格拼图开发一个自动拼图功能
希望通过这篇文章,抛砖引玉,帮助前端同学:
1,通过对算法的学习,对于数据驱动视图有更深入的了解
2,将算法和视图结合后,可以直观的了解算法的运行过程,避免了学习算法的枯燥
3,通过学习理解算法,可以让我们更好的理解框架,从而更好的使用框架,提高页面性能
题目说明
九宫格拼图,通过将一张图分成9张小图,打乱顺序后3X3排列,随机抽掉一张子图作为空白格,玩家每次移动空白格相邻的子图到空白格,不断通过移动,最终还原成原来的大图。
效果展示

问题分析:
九宫格拼图/数字拼图,其实就是八数码问题,给定一个初始状态和目标状态,求如何移动,完成从初始状态到目标状态
- 数据/视图拆分
首先要将视图与数据拆分开,分开后的9张小图,从1-9来表示,空白格用0来表示,这样问题就从怎样还原图片变成怎样还原数据的问题。
- 能否还原
首先有个问题,表示九宫格数据的数组,并不是每次随机打乱后,都能够还原成原始状态,就像魔方一样,正常魔方一定可以被还原,但如果将魔方的块扣下来,打乱后手动拼起来,就有很大的几率是无法被还原的,所以还需要判断是否能被还原,如何判断,则可以利用逆序对的来进行判断,
什么是逆序对,引用百度百科的解释:
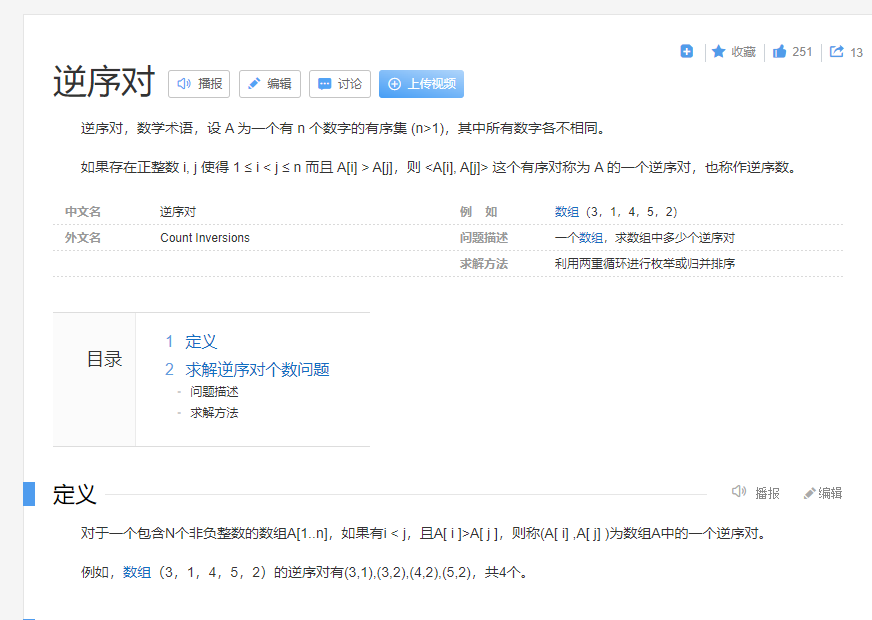
通俗点来说,就是一个数组里,如果一个排在前边的数A,跟在它后边的数B做比较,如果A>B,则数组的逆数对数量+1
如果两个数组的逆序奇偶性相同,则可相互转换,否则不可转换。
- 如何还原
假设将最后一张图作为空白格,还原成功后的大图,可以这样用数组表示:[1,2,3,4,5,6,7,8,0],只要将打乱后的数据,还原成这样,就表示拼图还原成功。
- 搜索算法
九宫格的结构包含行,列,本质上是属于数据结构图的一种,用数组表示,即[[1,2,3,],[4,5,6],[7,8,9]]这样的二维数组,每一个子数组表示一行,子数组的元素表示列,如果使用一维数组,需要针对行,列位置进行处理。
我们使用状态空间搜索算法,即将问题求解过程,解释成寻找从初始状态到目标状态的过程。
常用的状态空间搜索有深度优先搜索和广度优先搜索。
1,深度优先搜索 (Depth First Search)
简称DFS,一种用来遍历树或图的算法,策略是尽可能深的搜索树的分支。从根节点开始,从该结点的子结点一直搜索,直到该路径上的最后一个结点,然后再从未被搜索过的的相邻节点进行搜索,不断重复,直至所有结点都被搜索到,搜索结束。

2,广度优先搜索 (Breath First Search)
简称BFS,以广度优先进行搜索,是一种盲目搜寻算法,会展开所有节点,搜索结果,也就是说,不会考虑结果可能存在的位置,而是搜索所有节点,直到找到结果为止,先访问根节点,然后访问其子节点,然后再依次进行被访问点的子节点,就像枪靶一样,一层一层往外扩展,搜索完一层,再搜索外边一层,直至最外层,搜索结束。
关于两种搜索策略的理解
举个例子:你跟你的同学四个人,站在一个十字路口,需要去一个地方,但是不知道方向,这里有两种选择:
第一种选择:随机选择一个方向,然后四个人一起走,知道走到路的尽头,如果不对,回到十字路口,再选择其他方向尝试,知道找到目的地。
第二种选择: 四个人各自选择一个方向,每次大家同时往外走一步,如果没有找到目的地,然后再同时往外一起走一步,重复这个过程,知道找到目的地。
- 搜索算法与八数码问题
无论是DFS还是BFS,起始节点都是固定的,但八数码问题,每次操作的块并不都一样,所以用操作的块作为节点是不合适的,意味着起始节点一直在变化。
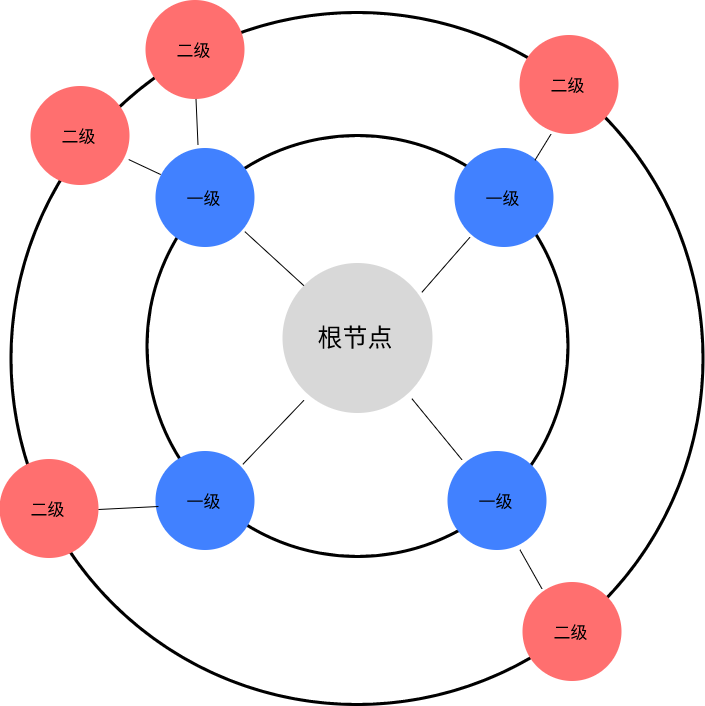
那么我们换个思路,将每次移动后9个块的位置状态作为一个节点,再跟正确顺序的状态作为节点做比较,是不是就可以了,同时每次移动之后,都会有三种或者四种后续移动方案,那么就相当于当前节点的后续子节点,如下图:

BFS和DFS有一个缺陷,都是在一个给定的状态空间范围内搜索,在状态空间不大的情况下比较适合,当状态空间比较大,而且不可预测的时候效率就会变低,而八数码问题的数据集,[1,2,3,4,5,6,7,8,0]总共有362880种排列组合,即9!种状态
考虑到时间和空间的限制,需要新的搜索策略,
- A*寻路算法
A*寻路策略,属于启发式搜索的一种,在状态空间中搜索时,对每一次搜索的状态进行评估,计算出最优的状态,再从这个状态进行扩展搜索,可以理解为广泛搜索+深度搜索,在搜索过程中,对每一种状态的估价是十分重要的,采用不同的估价会产生不同的效果。
估价函数:f(n) = h(n) + h(n)
f(n)表示节点n的估价函数
g(n) 表示在当前状态空间中,从初始节点到N节点的实际代价
h(n) 表示在当前状态空间中,从N节点到目标节点的实际代价
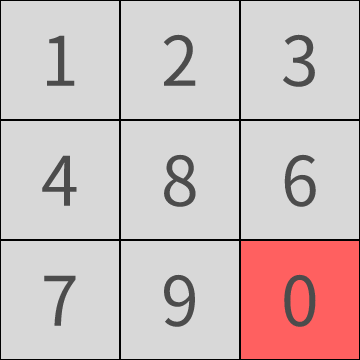
在八数码问题中,我们可以计算出每个块到达目标位置的曼哈顿距离,例如下图将数字8移动到数字0的位置只需要1步,而移动到数字6的位置,则需要2步,
结合上边的公式,每个块的估价f(n) = g(n) 从上一位置到当前位置的步数 + h(n) 从当前位置到目标位置
状态的估值 = 所有数字的估值之和

结合上边的说明,每次移动后,分别计算后续移动方案的估值,然后选择一个估值最小的方案继续搜索。
原理讲完了,下边上完整代码:
class BlockState {
//状态估值
f;
//从当前状态到下一状态的步数
g;
//下一状态到最终状态的步数
h;
blocks = [];
parentBlockState;
successBlocks = [1, 2, 3, 4, 5, 6, 7, 8, 0]
moveBlocks = [];
//拼图规格
rows = 3;
cols = 3;
moveStep;
constructor(blocks, parentBlockState) {
this.blocks = blocks;
this.parentBlockState = parentBlockState;
}
setMoveBlocks(from, to) {
this.moveStep = {
from,
to
}
}
//获取块的行列数据 一维数组需要特殊处理行列数据
getPlaceBlock(index) {
let row = Math.floor(index / this.rows);
let col = index < this.cols ? index : index % this.cols;
return { row, col };
}
//转成字符串
getBlockData() {
return this.blocks.toString();
}
//计算评估值
getF() {
this.f = this.f ? this.f : this.calcG() + this.calcH();
return this.f;
}
//计算从父状态到当前状态的步数
calcG() {
this.g = 0;
this.parentBlockState.blocks.forEach((e, i) => {
let p = this.getPlaceBlock(i);
let c = this.getPlaceBlock(this.blocks.indexOf(e));
this.g += this.calcDistance(p, c);
})
return this.g;
}
//从当前状态到完成状态的步数
calcH() {
this.h = 0;
this.blocks.forEach((e, i) => this.h += this.calcDistance(this.getPlaceBlock(i), this.getPlaceBlock(e == 0 ? this.successBlocks.length - 1 : e - 1)));
return this.h;
}
//计算距离,曼哈顿距离
calcDistance(from, to) {
return Math.abs(from.row - to.row) + Math.abs(from.col - to.col);
}
//扩展子状态
expand() {
let index0 = this.blocks.indexOf(0);
let childBlocks = [];
this.blocks.forEach((e, i) => {
//通过距离空位距离为1来查找后续的状态
if (this.calcDistance(this.getPlaceBlock(index0), this.getPlaceBlock(i)) == 1) {
let nextBlocks = _.cloneDeep(this.blocks);
[nextBlocks[i], nextBlocks[index0]] = [nextBlocks[index0], nextBlocks[i]];
let nextBlockState = new BlockState(nextBlocks, this);
nextBlockState.getF();
nextBlockState.setMoveBlocks(i + 1, index0 + 1);
childBlocks.push(nextBlockState);
}
})
return childBlocks;
}
//获取上级移动步骤
getSuccessMove() {
let moveSteps = []
let getParentMoveStep = (state) => {
if (state.parentBlockState) {
moveSteps.unshift(state.moveStep)
getParentMoveStep(state.parentBlockState);
}
}
getParentMoveStep(this);
return moveSteps;
}
}
class Robot {
openStateList = [];
closeStateList = [];
//开始数据组合
startBlocks = [];
//成功组合
successBlocks = [1, 2, 3, 4, 5, 6, 7, 8, 0];
constructor(startBlocks) {
this.startBlocks = startBlocks;
}
//运行
crackRun() {
console.log('开始还原')
//根据逆序对检查是否可还原
let copyStartBlocks = _.cloneDeep(this.startBlocks);
let copySuccessBlocks = _.cloneDeep(this.successBlocks);
let checkRes = this.checkCrash(copyStartBlocks, copySuccessBlocks);
if (!checkRes) {
throw new Error('当前拼图不可被还原')
}
let successState;
//初始化块
let startBlockState = new BlockState(this.startBlocks);
this.openStateList.push(startBlockState);
let isCracked = false;
while (this.openStateList.length > 0) {
let checkState = this.openStateList.shift();
this.closeStateList.push(checkState);
console.log('当前验证的状态', checkState.getBlockData())
if (checkState.getBlockData() === this.successBlocks.toString()) {
successState = checkState
isCracked = true;
break;
}
//扩展子状态
let childBlocks = checkState.expand();
if (childBlocks) {
//判断状态是否已经校验过
childBlocks = childBlocks.filter(e => this.closeStateList.findIndex(b => {
return b.getBlockData() === e.getBlockData();
}) === -1)
this.openStateList.push(...childBlocks);
//根据估值进行排序
this.openStateList.sort((a, b) => {
return a.getF() - b.getF();
})
}
}
if (isCracked && successState) {
let steps = successState.getSuccessMove();
console.log('成功解出,按照以下步骤还原')
return steps;
} else {
throw new Error('臣妾做不到')
}
}
//判断是否可以解出
checkCrash(startBlock, successBlocks) {
return this.inverseCount(startBlock) === this.inverseCount(successBlocks);
}
//计算逆序对 这里直接暴力查询,也可采用归并排序查询
inverseCount(blocks) {
let num = 0;
blocks.splice(blocks.indexOf(0), 1);
blocks.forEach((item, index) => {
for (let i = 0; i < index; i++) {
if (blocks[i] != 0 && blocks[i] > item) {
num++;
}
}
});
return num % 2 ? 1 : 0;
}
}
